Second-order fluid
An incompressible second-order fluid is the retarded-motion expansion terms through second order. The retarded motion expansion is one constitutive model to describe non-Newtonian fluids.
In a Newtonian fluid, the stress tensor τ is a function of the rate of strain tensor, 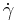 , proportional to the Newtonian viscosity,
, proportional to the Newtonian viscosity, 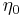 which is independent of shear-rate (the magnitude of the rate of strain tensor).
which is independent of shear-rate (the magnitude of the rate of strain tensor).
The retarded motion expansion expands the Newtonian definition, assuming the fluid is incompressible and the stress tensor is symmetric.
The first order expansion reduces the Newtonian definition above. The second order expansion can be written as
where 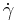 is the shear rate, and
is the shear rate, and 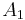 ,
, 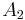 , and
, and 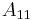 are coefficients.
are coefficients.
References
Bird, RB., Armstrong, RC., Hassager, O., Dynamics of Polymeric Liquids: Second Edition, Volume 1: Fluid Mechanics. John Wiley and Sons 1987 ISBN 047180245X(v.1)
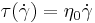
![{\tau(\dot \gamma)} = A_1 {\dot \gamma}^{(1)} %2B A_2 {\dot \gamma}^{(2)} %2B A_{11}[{\dot \gamma}^{(1)} \cdot {\dot \gamma}^{(2)}]](/2012-wikipedia_en_all_nopic_01_2012/I/9fca5a2d1d5d61fa55daf2baca850782.png)